【中学受験問題解説】 【必見】 都内進学校生が難関中学の算数の問題を徹底解説してみた 灘中1日目・編

Tweet

灘中算数の問題を流し見していったとき、面白い問題を見つけたので、皆さんに共有したいと思います。

ここでは、過去問集などに載っていそうな一番綺麗な解法に加えて、自分がこの問題を解いてみたときの思考の経路を記してみたいと思います。

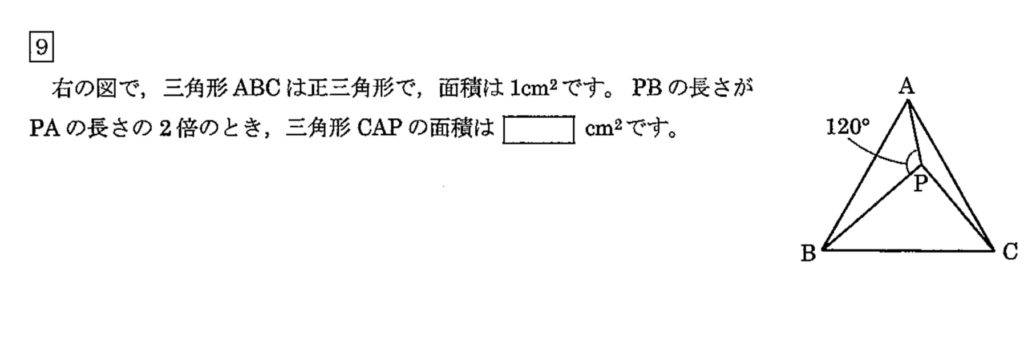
こちらの問題になります。僕はこのような、問題文が複雑でない綺麗な問題を見ると解いてみたくなるのですが、皆さんはどうですか？

この問題は幾何の問題なので、例題と言ってもあまり関連する問題は作れません。今回も一応例題を作りますが、この問題とはあまり関係ありません。

例題:シュタイナー点

鋭角三角形（全ての内角が90°未満の三角形）ABCがあります。点Pをこの三角形の辺上または内部にとったとき、AP+BP+CPの長さが最小になるとき、
角APB=角BPC=角CPA=120°
になることを示せ。ただし、XYで線分XYの長さを表すものとする。

シュタイナー点と呼ばれる問題になります。この定理自体の使用頻度はほぼ0ですが、証明方法は他分野に応用が効きます。しかし、上にあげた灘中の問題よりもこちらの例題の方が難しいかもしれません。

パッと思いつかなければ下の答えを見ていただいて結構です。自分の算数力に自信があるなら、チャレンジしてみてください。

例題の解答

折れ線の長さの和は、求めるのがとても難しいものの１つと言われています。高校に入ってベクトルという分野を習うまでは、折れ線の長さを折れ線の長さのままゴリ押しで解くのは結構大変です。

そこで、折れ線の長さの和の最小を求めるためには、折れ線を移動して直線にすればいいのです。

何を言っているのかさっぱりな人もいると思うので、下の図を見てください。

補題（というほどのものでもないですが）

補題の解答

定点A、Bがあり、A、Bを中心とする円上にそれぞれ点C、Dがある。AB=1、AC=0.3、BD=0.4のとき、CDの長さの最小値を求めよ。

AC+CD+DBの長さの最小値は、A、C、D、Bが全てこの順に一直線上の時で、最小値は1。よって、CDの長さの最小値は、1-0.3-0.4=0.3。

超簡単ですね。同じ折れ線の長さのはずなのに何が違うのでしょう？

そう、「全てこの順に一直線上の時」というワードが使えるかどうかが違いなのです。

では、上の例題の方もこのキラーワードが使えるように、変形してしまいましょう。

AP、ACを一辺とする正三角形をBと反対側に作ります。

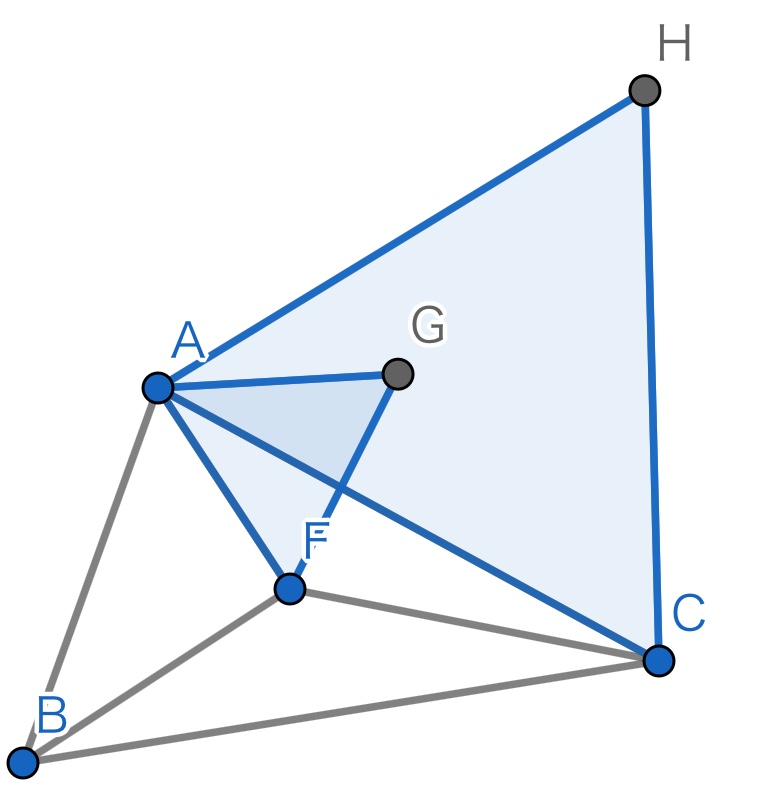
ここで、FGはAFと同じです。さらに、AF=AGかつAC=AHかつ、角FAG=60°-角GAC=角GAHより、二辺夾角相等で、三角形GAHは、三角形FACを反時計回りに60°回転しただけだとわかります。

すると、GH=FCとなります。よって、FA+FB+FC=AF+FG+GHとなり、折れ線の長さの和になりました。

BとHは定点なので、この長さの最小はB、F、G、Hがこの順に同一直線上の時とわかります。ようやくキラーワードが出てきました。

さて、B、F、G、Hが同一直線上になどなるのでしょうか？

これはなります。まず、角AFGは60°なので、B、F、Gが同一直線上になるためには角AFGが120°が必要で、同様にF、G、Hが一直線上になるためには角AGH =角AFCが120°が必要ですね。（証明終わり）

この問題は、結局三角形AFCを反時計回りに60°回転することで解決されました。60°回転は正三角形をいくつも生み出すので有用なことが多いです。

ではいよいよ灘中1日目の問題の解答に行きましょう。

今回の問題

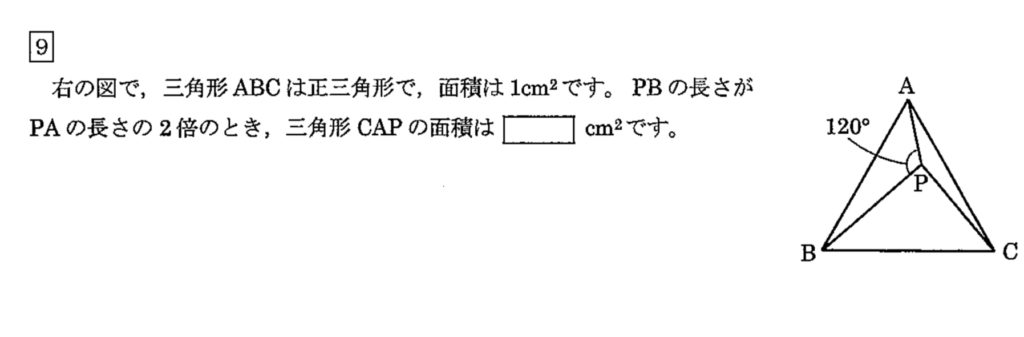
こちらの問題でしたね。

まず、多くの過去問集などがあげているであろう、綺麗な結論からお見せします。

参考書的解答

下の図のように補助線を引くと、７つの三角形全て面積が等しい。よってその1個の面積は1/7㎠。なお、XはPBの中点、YはXCの中点。

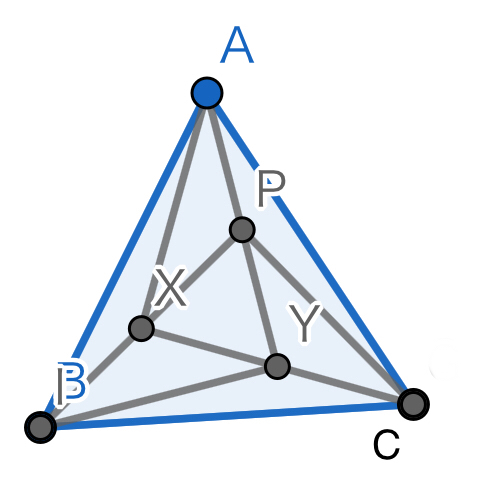
ここまで不親切な解答集はないとしても、多くにはこれに類する、思いつかないと解けない系の解法しか載っていないと思います。無論そういう問題は思いつきこそが大事で、思いつかないと解けないことが多いです。しかしどうやって思いつくのかわからない人も多いことでしょう。

では、ここからはこの解答を導き出した際の僕の思考回路をお見せします。このような思いつき系の問題を解く一助になればと思います。

僕の思考

僕もぱっと見では上の解法など全く思いつかなかったので、とりあえず60°回転を試してみました。三角形全体を60°回転したものを書き加えると、下のようになりました。

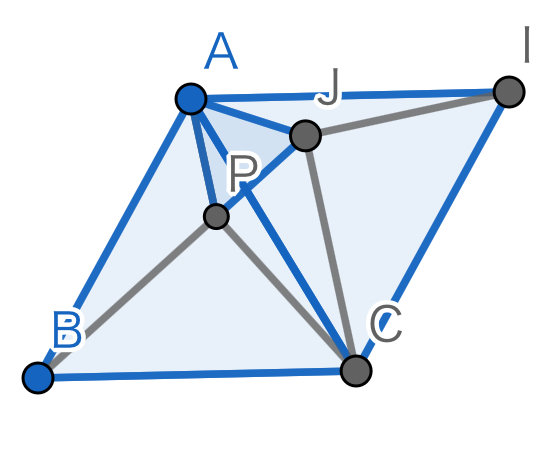
すると、先ほどと同じようにB、P、Jが一直線上ですね。また、角BJCは120°-60°=60°となります。すると、BPの中点を取りたくなりますね。BPの中点をXとすると、XJ=AP+BP/2=BP=JCとなり、三角形JXCが正三角形になるからです。とってみましょう。

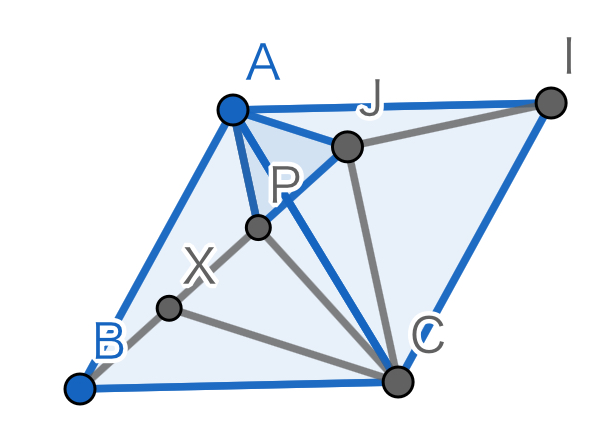
すると、BX=AP、XC=BP、BC=ABなので、三辺相等で三角形APBとBXCは合同になります。

また、APとJCは平行で、AJとXCも平行なので、APを伸ばしてXCとの交点をYと置くと、四角形AYCJは平行四辺形です。ここで、YC=AJ=AP=BP/2=XC/2なので、YはXCの中点でもあるとわかります。図は下にあります。

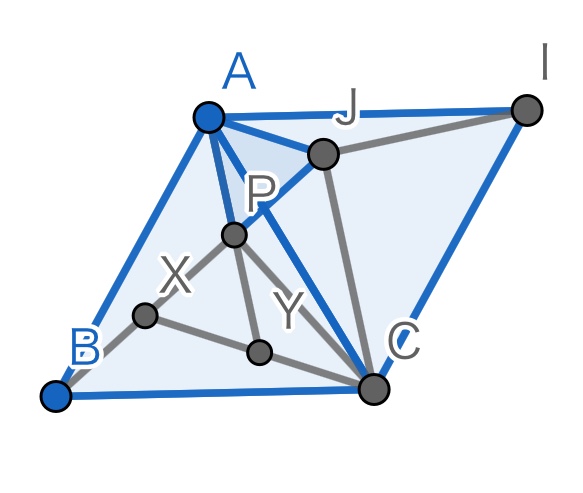
すると、PX=PY=XYなので、三角形PXYは正三角形になります。さらに、AY=AP*2=BP、YC=PA、CA=ABなので、三辺相等で、三角形AYCもBPCと合同です。

また、三角形PXYの面積を①と置くと、三角形PYCは高さが共通で底辺の長さは等しいので面積は①になります。同様に考えて三角形APCも①になります。すると、三角形AYCは②になります。よって合同な三角形である三角形BPAもCXBも②ずつとなります。

よって全体は⑦になります。求める面積は三角形APCなので、①です。よって1㎠/7=1/7㎠、となります。

お分かりいただけたでしょうか？

今日のポイント

• 60°回転は有効なことが多い
• 折れ線の長さの和の最小を求めたければ直線になるように折れ線を動かす
• 思いつき問題に慣れるには、練習あるのみ！

例えば60°回転などのテクニックを学ぶためには、とにかく演習を積むことが大事です。僕もどちらかといえばドリルは嫌いですが、それをやったことで合格できたし、学力が伸びたことは否めません。この記事をきっかけに皆さんがたくさんのテクニックを学ぶために、演習を積んでくださることをお勧めします。

参考ページ一覧：こちらの記事もぜひお読みください！

この記事を書いたライター

東京受験

• インタビュー2021年11月20日【13の質問】あなたが医学部受験を決める理由＆受かる人の特徴とは？－医学部受験塾ACE Academy社長髙梨裕介さんインタビュー
• 受験対策・科目別勉強2021年9月18日「医学部予備校ACE Academy」体験記
• 勉強法&生活スタイル2021年7月29日【超必見】楽器練習ガチ勢へ。
• 豆知識・思うこと2021年7月1日【創立100周年！】中国共産党ってどんな党？

Tweet