中学受験算数で役立つ小学校で習わない高等テクニック　①数学的帰納法・編

Tweet

みなさん、中学入試算数の解答を読んでいて、「こんなテクニックあったんだ」などと感心したことはありませんか？

解答解説を書いているのは中学受験のプロである大人たちです。そんなプロたちはもちろん中学、高校を卒業しているわけですから、中学や高校で習うようなテクニックも知っています。それらを使うと、中学受験の算数は簡単に解けてしまうことがあります。

もちろんそんなテクニックを使わない解答もあるのですが、時間がかかったり、計算量が増えたり、あるいは発想力が求められたりします。

そんな時のために、これから現役高校生の僕が中学受験で役立つ高等テクニックをいくつか皆さんに伝授したいと思います。

コラム紹介

このコラムでは、中学以上で習う数学のテクニックで、受験算数に役立つものをまとめていきます。

第一回は、数学的帰納法（すうがくてききのうほう）について学んでいきたいと思います。名前に算数ではなく数学とあることからもわかるように、主にこれは中学から高校の間で習うテクニックになります。

数学的帰納法って何？

辞書的定義

1．帰納法
① 多くの特殊的な事実から蓋然的(がいぜんてき)に真の一般的な原理、法則を発見する研究方法。ベーコンによって意味づけられ、Ｊ=Ｓ=ミルによって大成された。狭義では、ミルの定式化した因果関係確定の五つの方法をいう場合もある。帰納的三段論法。帰納的推理。⇔演繹(えんえき)法。
※百学連環（1870‐71頃）〈西周〉二「ミル氏の発明せるシストム ヲフ ロジックに至ては Induction （帰納法）に依て此学を極るとなし」
② 論理学で、帰納のための一時的な手続きがあるとする人がこの手続きを呼ぶときの名。 (小学館　精選版　日本国語大辞典『帰納法』より）

2．数学的帰納法
〘名〙 数学における証明法の一つ。自然数（1以上の整数）に関するある条件について、自然数１がその条件を満たす、自然数ｎがその条件を満たせば n+1 もその条件を満たす、という二つのことが成立するならば、いかなる自然数もその条件を満たすという原理に基づくもの。完全帰納法。
(小学館　精選版　日本国語大辞典『数学的帰納法』より）

はい。何を言っているのかさっぱりですね。では簡単に説明しましょう。

一般に、帰納法と数学的帰納法は全く別のものだと言われています。そのため、数学的帰納法だけを説明していきます。

例題を用いた説明

例題1：

日本の祝日法では、祝日と祝日に挟まれた日は休日とするとされている。
一方で、架空の国USCの祝日法が改正され、祝日の次の日は祝日と決まった。
さて、USCで元旦（1月1日）が祝日であるとすると、どのようなことが起こるか。

さあ、元旦を迎えました。祝日です。しかし、祝日の次の日は祝日ですから、1/2も祝日です。おや、1/3も祝日…とうとうこの国では、1年中祝日になってしまいました。もちろんみんな長期休暇で遊びまくりです。当然会社は破綻し、人々は路頭に迷い、、etc.

ということで正解は、みんなが不幸になる、ではなくて、次の元旦以降ずっと祝日になる、でした。

このように、一つ前がある条件を満たす（ここでは祝日である）と仮定すると、その次も同じ条件を満たすことを利用して、無限に続くことを証明してしまおうというのが、数学的帰納法です。

では、例題2に行きましょう。今度は算数です。

例題2：

1,2,3….□まですべて足すと、□*(□+1)/2となることを示せ。

数学的帰納法を用いるときに示さなければならないのは次の2つです。

1. 最初（1個目）において成り立つことを示す。
2. ☆個目が成り立つことを仮定して（☆+１）個目が成り立つことを示す。

これらを使って示していきます。

まず□＝1の時、1=1*(1+1)/2となり示せました。

次に1+2+3+…+☆＝☆*(☆+1)/2より、
　　1+2+3+…+☆+(☆+1)=(☆*(☆+1)/2)+(☆+1)=(☆+1)*((☆/2)+1)
=(☆+1)*((☆+1)+1)/2となり、これは□に(☆＋1)を入れたものになっている。よって数学的帰納法より示されました。(証明終わり)

このようにめんどくさそうに見える問題も考えずに一発でとけてしまうのが数学的帰納法のいいところです。

発展: 一筆書きの可能性の証明

ここからは、筑波大附属駒場中学の算数でも出題された、一筆書き問題を数学的帰納法を使って解いていきたいと思います。

問題はこちら

点(島)につながる辺(橋)の数がすべて偶数本の時、（図形自体が２つに分かれているときは除く）必ず一筆書きできることを示していきます。

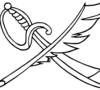
こんな感じの図形があったとします。きちんと各点につながる辺の数は偶数本ですね。この図形が一筆書きできるかどうかを調べていきます。

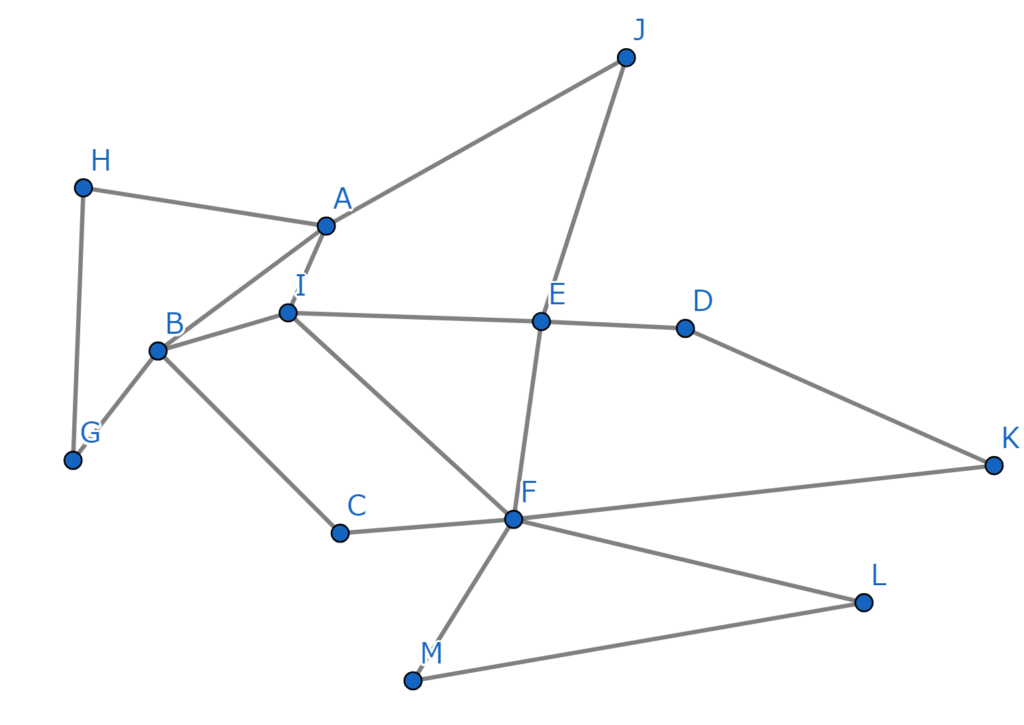
まず、辺が2本しかつながっていない点がありますね。例えば、点Hです。こうしてみたらどうでしょう。

もしこれで一筆書きできるなら、上の図形でも一筆書きできることになります。

まったく同様に、辺が2個つながる点はサクサク消せますね。

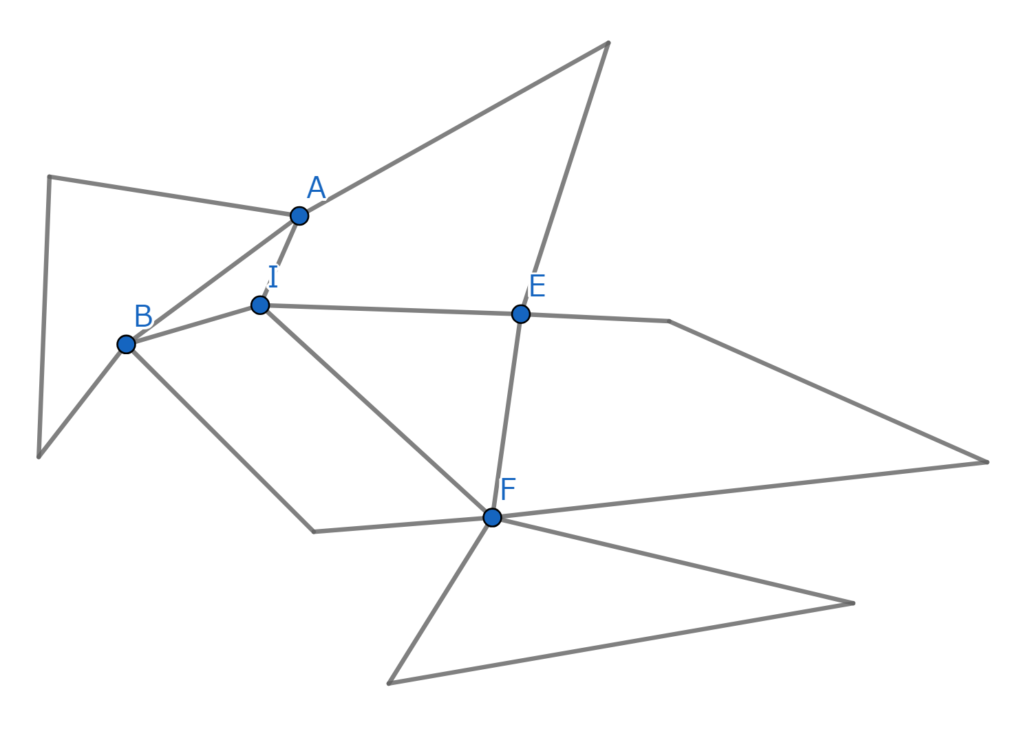
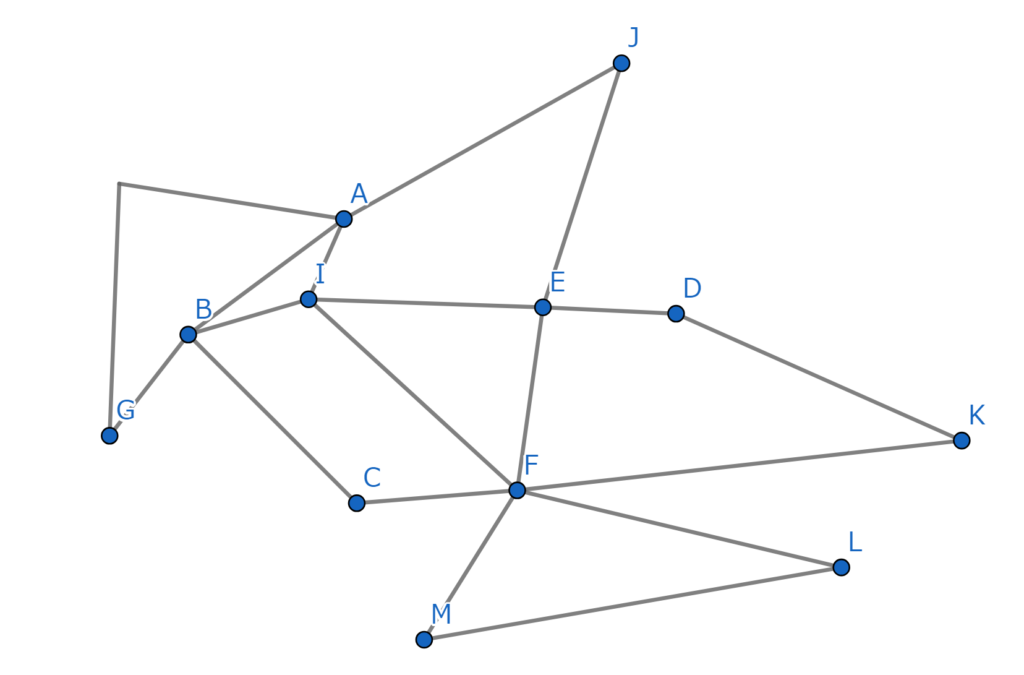
点が一気に五個まで減ってしまいました。見やすくするためにこの図形を、どの点とどの点の間に何本辺があるかを変えずに書き換えてみましょう。するとこうなります。

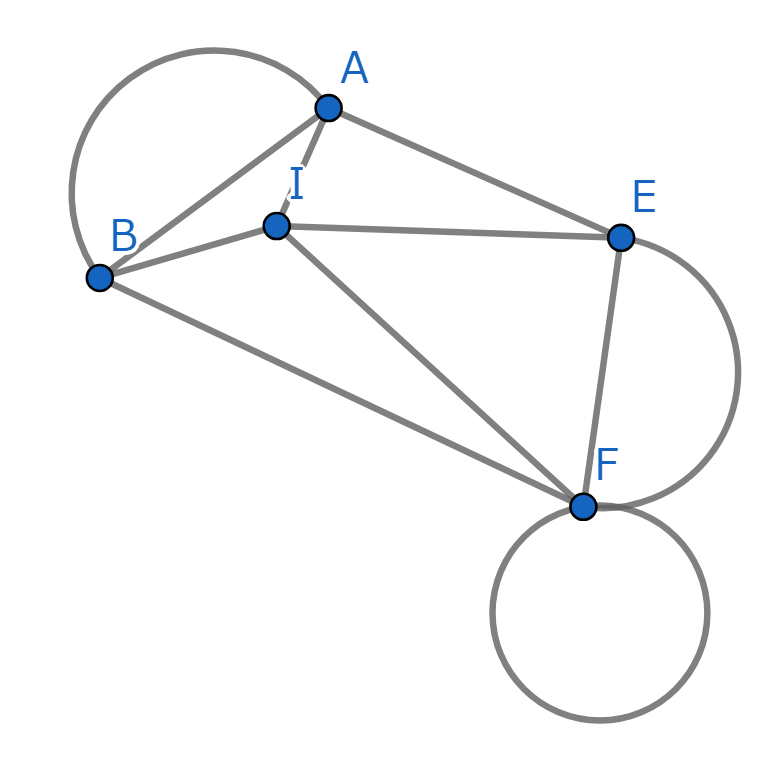
だいぶ見やすくなりましたね。この図形が一筆書きできるなら、最初に挙げた図形も一筆書きできることが分かっています。しかしいよいよここからが本番です。辺が4本以上つながる点を消して、消した後の図形が一筆書きできるなら消す前の図形も一筆書きできることを示します。

点Eに注目しましょう。点Eを半分に切るイメージで左右に引き離すと下の図形になりますね。

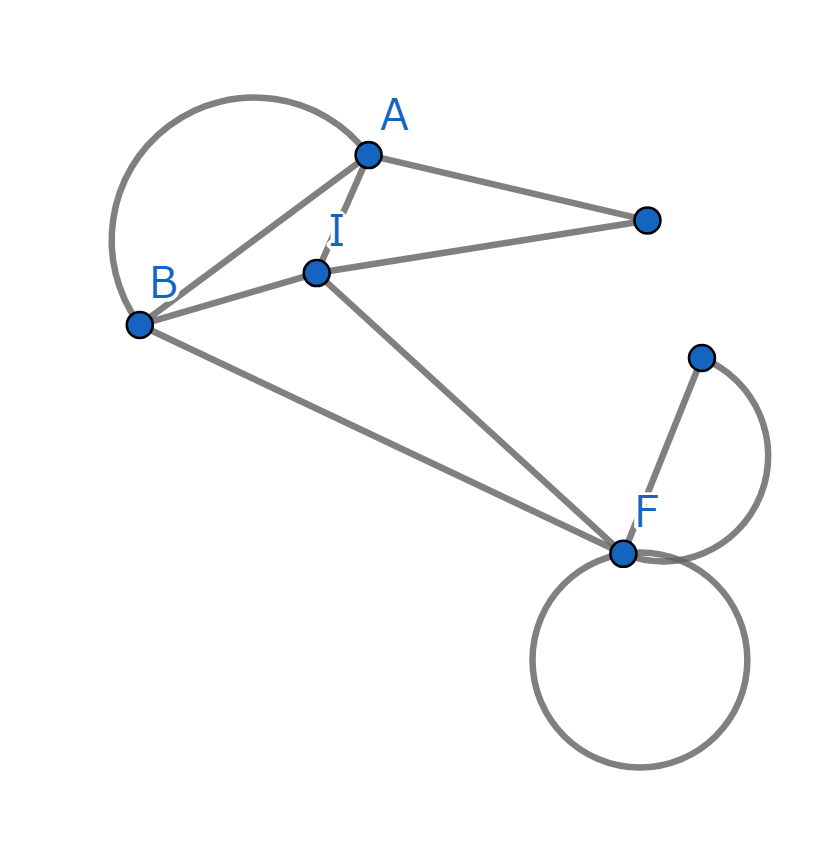
もしこの図形が一筆書きできるなら、先ほどの図形も一筆書きできますね。ここでよく見ると、辺が2本しかつながっていない点ができていますね。では消して整理してみましょう。

さあ、また点が一つ減りましたね。ここで点Fを見ると、辺は6本出ているように見えますが、他の点とつながっている辺は2本だけです。これは見せかけで6本出ているだけと考えることができますね。Fについたら、この円形の道2本を通ればいいだけですから。よってFも消せます。

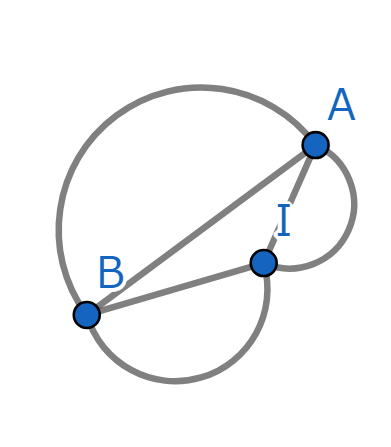
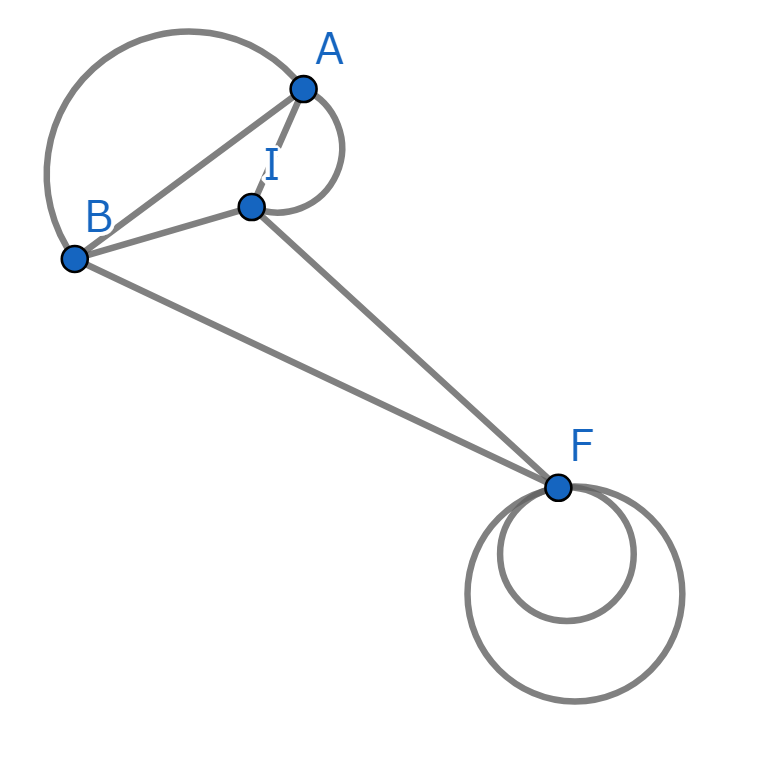
図形はこんなに小さくなりましたが、これを一筆書きできるならば最初の図形が一筆書きできることは示されています。ではいよいよ大詰めです。BとIも消しましょうか。

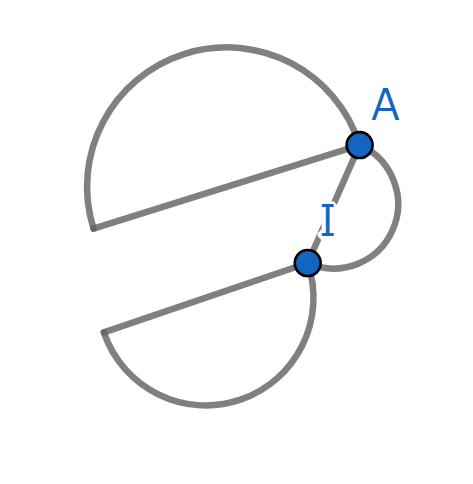
これでBも消えました。ここでIは見せかけの４本とわかるので、これもすぐ消えます。

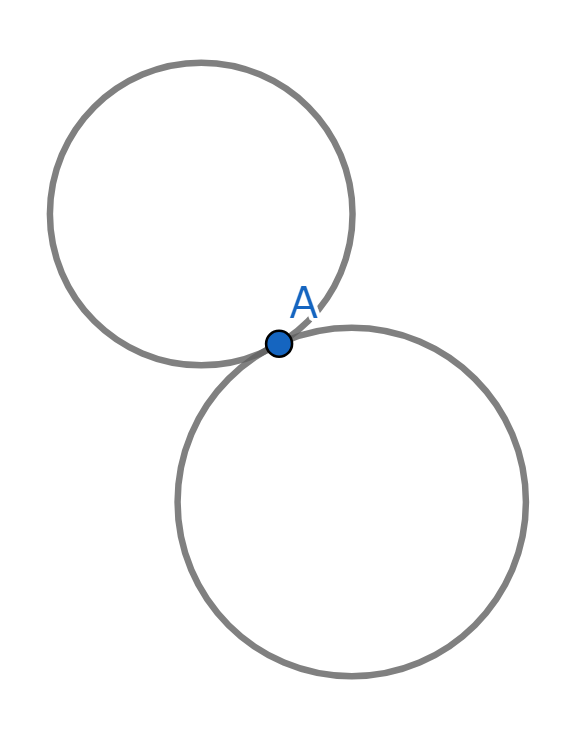
ついに一点だけになってしまいました。しかしこの図形の作り方から、この図形が一筆書きできるなら最初の図形も一筆書きできますね。

しかし、一点のみの図形が一筆書きできるのは自明なので、結局最初の図形も一筆書きできる、とわかりました。

さあ、ここでようやく数学的帰納法の出番です。

今見せたように、最初点が□個ある図形が一筆書きできるかどうかを調べるときに、一つずつ点を消していきました。

つまり、ある点が□ー１個の図形であって、その図形が一筆書きできるならば、最初に問題で与えられた点が□個の図形も一筆書きできるとわかるようなものがが存在する、ということが示せたのです。ここが重要です。

よって、次に点が□－１個の図形に対しても、点が□―2個の図形であって、その図形が一筆書きできるならば、さっきの点が□－１個の図形も一筆書きできるとわかるようなものがが存在するのです。

こうしてだんだん図形の点の数は小さくなっていって、最後には「点が1個の図形であって、その図形が一筆書きできるならば、その前の点が２個の図形も一筆書きできるとわかるようなものがが存在する」 とわかります。

これは、「ここに出てきた点が☆個の図形が一筆書きできるなら、その一つ前に出てきた点が☆＋１個の図形も一筆書きできる」ということを示しています。

点が1個の図形が一筆書きできるのは自明なので、この２つから数学的帰納法より、点につながる辺の数がすべて偶数本の時、（図形自体が２つに分かれているときは除く）必ず一筆書きできることが示された。

ところで気になっている人もいるであろうこの文、「図形自体が２つに分かれているときは除く」ですが、簡単な話で、以下の図のようなときは一筆書きなんてもってのほか、という意味です。

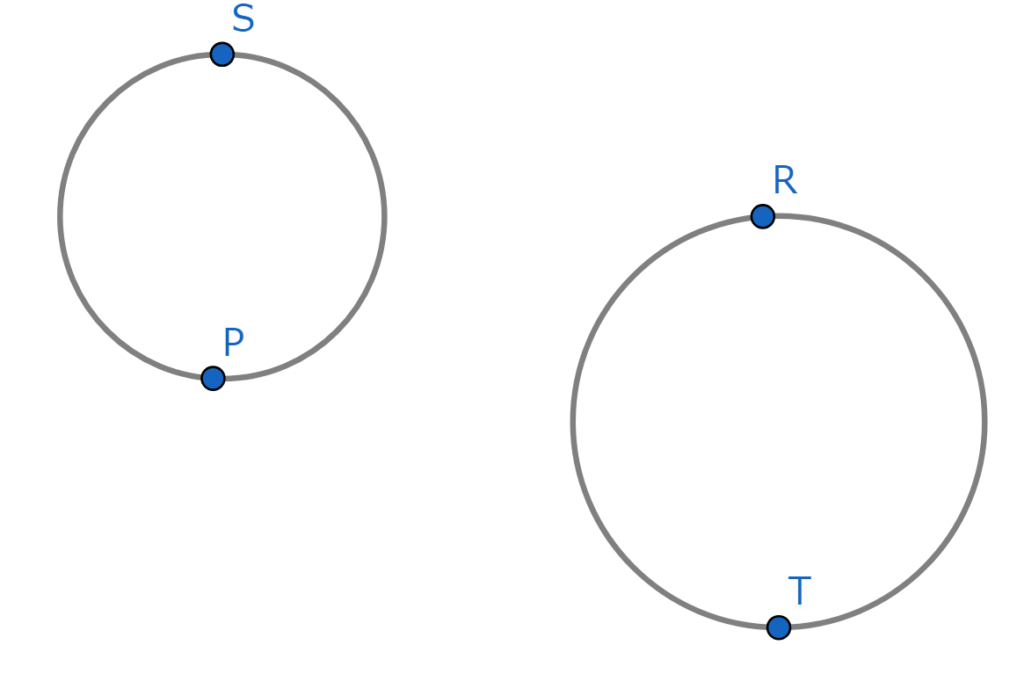
これは確かに各点に2本ずつ辺が入っていますが、一筆書きできませんよね。

点を二つに分けるときも、このように図形を二つに分けてしまう分け方はだめです。図形を二つに分けない点の分け方があるという証明は結構簡単なので、自分で考えてみてくださいね。

練習問題

数学的帰納法を使う問題自体はしばしばあります(上の筑駒中の例のように)が、数学的帰納法単体の問題を作ろうとすると、大抵□(はこ)の入った問題になってしまい、出題者側は出しにくいです。

数学的帰納法に慣れるために、練習問題はとりあえず□を使うものを出してみたいと思います。

問題

1から□までの平方数を全部足して6倍すると、□×(□＋１)×(2×□＋1)になることを示せ。

解答

まず、□が1の時、6＝6となり成立。

☆の時成立したとして、1から☆＋１までの平方数をすべて足すと、
☆×(☆＋1)×(2×☆＋1)＋(☆＋1)×(☆＋1)となります。これは計算すると、(少し大変ですが)　(☆＋1)×((☆＋1)＋1)×(2×(☆＋1)＋1)となっています。よって数学的帰納法より、これは成立します。(証明終わり)

大変なのは計算だけだ、とお分かりいただけたでしょうか。

まとめ

数学的帰納法は、今のうちから知っておくと中学受験だけでなく、その後算数から数学に変わった後の勉強もこの上なくはかどること間違いなしです。この機会に数学的帰納法をマスターして、数学の世界に一歩足を踏み入れてみませんか？

この記事を書いたライター

東京受験

• インタビュー2021年11月20日【13の質問】あなたが医学部受験を決める理由＆受かる人の特徴とは？－医学部受験塾ACE Academy社長髙梨裕介さんインタビュー
• 受験対策・科目別勉強2021年9月18日「医学部予備校ACE Academy」体験記
• 勉強法&生活スタイル2021年7月29日【超必見】楽器練習ガチ勢へ。
• 豆知識・思うこと2021年7月1日【創立100周年！】中国共産党ってどんな党？

Tweet