【こども支援】医学生が無料で勉強を教えます
エースアカデミーこども支援部では、長期休みのこどもを対象に教育支援企画を行っています！
医学生によるマンツーマン指導（オンライン個別指導）を完全無料で受講いただけます！
＊医学生の指導料はエースアカデミーこども支援部が全額負担。
お申し込みは公式LINEにて行いますので、ご登録のうえ案内をお待ちください！
【医学部に興味がある人必見】受験資料をプレゼント！
医学部受験に必要な資料集を無料でプレゼント中！
資料内容（合計8個）
医学部偏差値ランキング、共通テスト情報、
医学部に合格するための参考書一覧etc..
さらに、医師が解説するウェブセミナー動画もプレゼント！
初めましての方は初めまして、ライターの諏訪井です。前編を読んで後編も読もうと思ってくださった方、ありがとうございます！前編でおちゃらけすぎたので、こっちはめっちゃ真面目にやります。
前置きが面倒臭い早速本題に入りましょう。
3問目
問題
解答
(1)ア: 4通り イ: 9人
(2)①12 ②199 ③9 ④7 ⑤5 ⑥3 ⑦6 ⑧129
解説
僕は昔から場合の数が大好きな変な奴だったのですいすい解けましたが、多分受験生視点だとかなり敬遠したい問題だったと思います。なんか文章も長いし、解答欄も多いし。しかし落ち着いてやれば大して難しくもありません。
さて、見ていきましょう。今回は小問ごとに区切ってみようと思います。
(1)ア
| 10円 | 5円 | 1円 | 合計枚数 | 判定 |
| 2 | 1 | 3 | 6 | 〇 |
| 2 | 0 | 8 | 10 | 〇 |
| 1 | 3 | 3 | 7 | 〇 |
| 1 | 2 | 8 | 11 | ✖ |
| 0 | 5 | 3 | 8 | 〇 |
| 0 | 4 | 8 | 12 | ✖ |
以上より4通り。
(1)イ
1人が出す1円玉の数は3枚か8枚。よって、つるかめ算より1円玉を8枚出したのは9人。そして1円玉を9枚出すということは5円玉を出さないということだから、答えは9人。
(2)一番簡単なのは表を完成させる方法。
| 1 | 1,5,10 | 3 |
| 2 | 2,6,11,15,20 | 5 |
| 3 | 3,7,12,16,21,25,30 | 7 |
| 4 | 4,8,13,17,22,26,31,35,40 | 9 |
| 5 | 9,14,18,23,27,32,36,41,45 | 9 |
| 6 | 19,24,28,33,37,42,46 | 7 |
| 7 | 29,34,38,43,47 | 5 |
| 8 | 39,44,48 | 3 |
| 9 | 49 | 1 |
この表は実はかなり簡単に出来て、上の項の結果を利用すれば良い。上の項に例えば17があれば当然だが1つ下に必ず18が入る。5の倍数だけ上に行くことに留意しさえすればすぐにできるだろう。
①：389＝100×3＋50×1＋10×3＋5×1+1×4より、12。
②：1×4＋5×1＋10×4＋50×1＋100×1＝199
これは合計枚数が11枚なので条件に合う。
③：９
④：７
⑤：５
⑥：３
⑦：この問題を解くには表がもう1つ必要である。それは、50円と100円だけ考えた以下のような物だ。（見方は上と同じ)
| 1 | 50,100,500 | 3 |
| 2 | 150,200,550,600 | 4 |
| 3 | 250,300,650,700 | 4 |
| 4 | 350,400,750,800 | 4 |
| 5 | 450,850,900 | 3 |
| 6 | 950 | 1 |
見やすいように300以下の値には下線をつけた。以上2つの表より、
2×0＋2×1＋1×(1＋3)＝6(それぞれ和が11以上になるよう上下の表から数を選ぶ順列)
⑧：以上2つの表から
4×1＋4×(1＋3)＋4×(1＋3＋5)＋3×(1＋3＋5＋7)＋1×(1＋3＋5＋7＋9)＝129
しっかり表が書ければ簡単に解ける。
4問目
問題
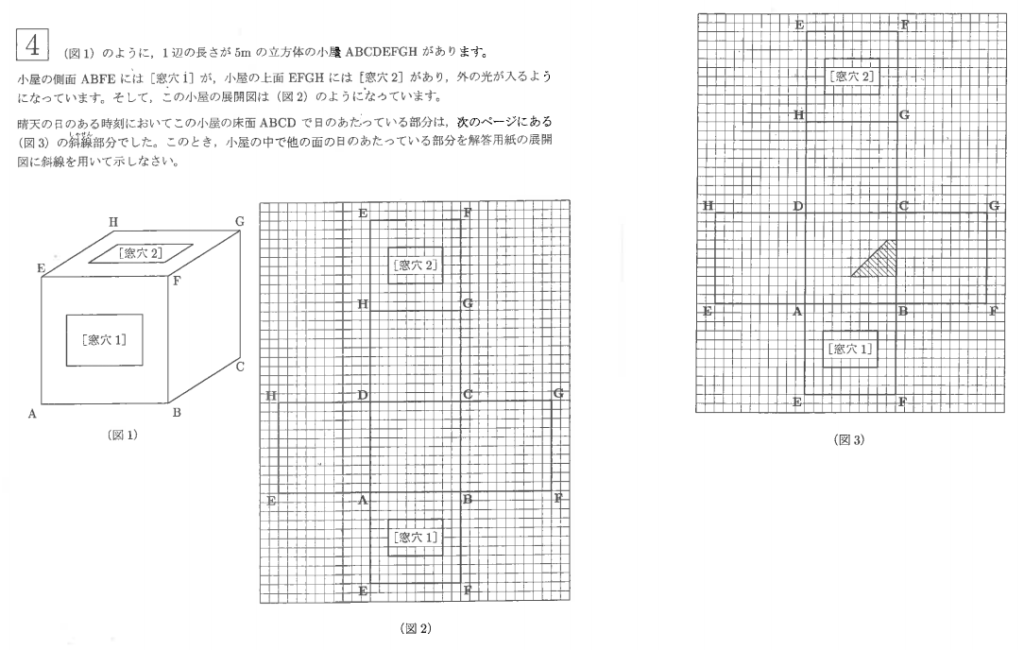
解答
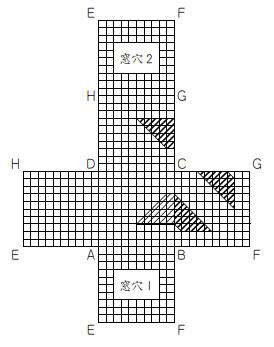
解説
この問題だけはかなり難しいです。正直な話僕はこれを改めて解く際にイライラして展開図を素手で切り取って考えました。
さて、ある程度の考え方ですが分かることとして①床の光は窓穴1を通過したものである、ということが大前提です。もしこれが窓穴2を通過したものだとすると太陽が約90°くらいで差してることになりますし、そもそもやってみたら分かりますが不可能でした。
ということは②太陽光が差す角度が分かりますね。具体的には丁度立方体の最も長い対角線と同じ角度、1×1×1の傾きです。
すると後はやるべきことは単純で、全ての穴からその光を通せばいい筈です。
この問題にも言えますが、開成の算数は(イメージですが)何をすればいいかは単純明快、でもそれを実践するのが難しいというタイプの問題が出やすい傾向にある気がします。開成を志望する生徒さんはしっかりとこうした作業力を身につけて下さい。
まとめ
前編でも書きましたがもし僕の解説に間違い等発見したとき、または質問等がございましたら東京受験.jpにご連絡下さい。諏訪井はちょっとびっくりしてから読者からの便りに大喜びするでしょう。それでは。
この記事を書いたライター
インタビュー2021年11月20日【13の質問】あなたが医学部受験を決める理由＆受かる人の特徴とは？－医学部受験塾ACE Academy社長髙梨裕介さんインタビュー
受験対策・科目別勉強2021年9月18日「医学部予備校ACE Academy」体験記
勉強法&生活スタイル2021年7月29日【超必見】楽器練習ガチ勢へ。
豆知識・思うこと2021年7月1日【創立100周年！】中国共産党ってどんな党？
【こども支援】医学生が無料で勉強を教えます
エースアカデミーこども支援部では、長期休みのこどもを対象に教育支援企画を行っています！
2021年度はのべ200人以上のこども達に、医学生による個別指導を届けることができました。
＊医学生の指導料は全額エースアカデミー こども支援部が負担しています。
こちらの企画では医学生によるマンツーマン指導（オンライン個別指導）を完全無料で受講いただけます！
受付開始のご案内、受講のお申し込みは公式LINEにて行いますので、LINEにご登録のうえお待ちください！
【医学部に興味がある人必見】受験資料をプレゼント！
医学部受験に必要な資料集を無料でプレゼント中！
資料内容：偏差値ランキング、共通テスト情報、医学部に合格するための参考書一覧etc..
合計8個の医学部入試の最新資料（PDF）を無料でご覧いただけます。
さらに、医師が解説するウェブセミナー動画（合計7時間以上）もプレゼント！
300名以上の医学部合格者を指導してきた医師が、医学部に合格するポイントを解説します。
