【中学受験問題解説】 【必見】 都内進学校生が難関中学の算数の問題を徹底解説してみた 開成中・編

Tweet

中学入試算数の名問を取り上げ、現役高校生が解説するこのコーナーも、今回で2回目となりました。今回は、私立の名門中の名門、開成中学の算数からこんな問題を取り上げて解説していこうと思います。

このコーナーの紹介を見たい方はこちら

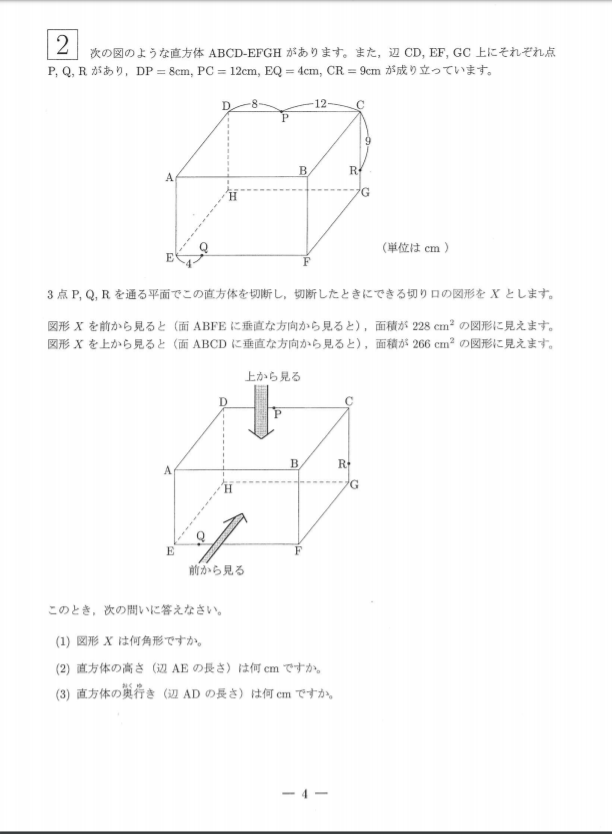
こちらは、立体感覚を問う問題の中でも、あまり見ないタイプの問題です。立体の切断面に関する問題は、扱ったことがあるかないか、あるいは問題演習の経験値によって大きく得点が分かれてしまいます。一方で、演習さえ積み、経験値を高めていくことで、確実に得点源にすることができる分野でもあるので、未習の人はこれを機会に問題演習を積むのもいいかもしれませんね。

まずは、立体感覚を養うことから始めましょう。こちらの例題からスタート！

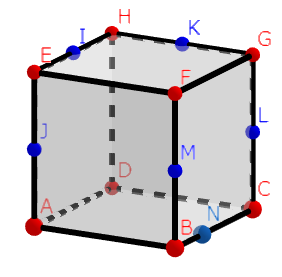
例題：立方体の切断

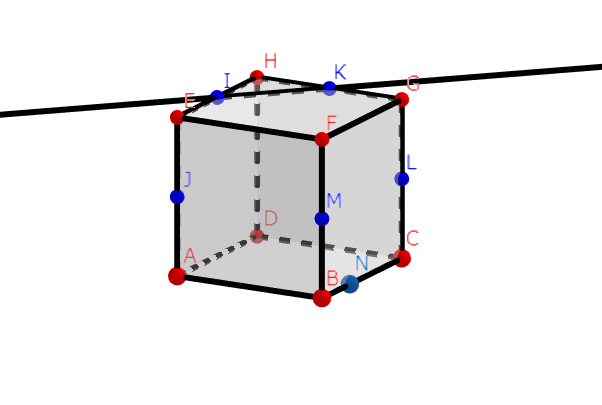
上の立方体ABCD-EFGHにおいて、青い点は各辺の中点であるとする。また、
点NはBN：CN＝１：２であるような点であるとする。
このとき、
（１）（超基本）3点J,M,Lでこの立方体を切ったときの断面の形は？
（２）（超基本）3点B,E,Gでこの立方体を切ったときの断面の形は？
（３）（基本）3点H,J,Bでこの立方体を切ったときの断面の形は？
（４）（やや難）3点I,J,Lでこの立方体を切ったときの断面の形は？
（５）（やや難）3点I,K,Mでこの立方体を切ったときの断面の形は？
（６）（難）3点K,J,Nでこの立方体を切ったときの断面の形は？

もちろん、勘で当たっても正解にはなりませんよ～

もちろん、こんなの全部即答！なんて方は読み飛ばしてもらって結構です。
しかし、立体の切断面を扱ったことがない人にとっては、（３）か（４）あたりからだんだん迷いが出てくるのではないでしょうか？　

また、（５）まではセンスで解けても、（６）は過去に類題を扱ったことがないと解けないと思います。逆に、これを初見で解ける人は天才だと思います。

立体切断問題　3つの原則

立体の切断面の問題で、もっとも根底にある原則は３つあります。

原則１：平面は通る３点を決めれば決まる
直線は通る２点で決まるように、平面は通る３点で決まります。
自分の下敷きとかを指３本で持てるのと同じことですね。

原則２：平面と平面の交線は直線
これは板チョコを、きれいに包丁で切ることを想像してください。普通にまっすぐ切れたら、直線になりますね。あるいは、平面と平行に包丁を振ってしまっては、交わらないという場合もありますね。

原則３：平行な２つの面に表れる切断面（直線）は互いに平行
ここが一番わかりにくいですね。立方体や直方体において、対面（向かい合う面）は互いに平行です。（このような性質を持ち、かつ六つの面を持つ立体のことを平行六面体といいます。直方体や立方体は平行六面体の一部です。）
今度は、四角いケーキを包丁で切ることを考えてみてください。
これはイメージではどうしようもない部分があるので、上の問題の（３）を解きながらゆっくり解説します。

それでは例題の解答に行きましょう。

例題の解答

（１）この問題はセンスで分かる人も多いでしょう。というか、センスで解くほどの問題でもありません。

また、板チョコや直方体の面は有限なので、切断面が平面と平行ではなくても、交線が現れないことがあります。

では（１）。これは立方体をちょうど真ん中で切った、というだけですね。

切断面は皆さんの予想通り、このようになりまして、正方形、が正解になります。

つづいて（２）。こちらは、切断面が各面上に線分として現れることが分かれば余裕ですね。

EとG、GとB、BとEをそのままつないでできた下の図のようになります。

できたのは三角形ですが、三辺の長さは等しいので、正三角形が正解となります。

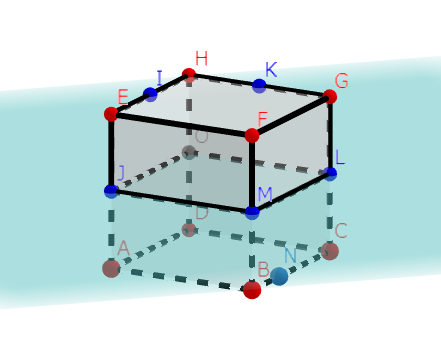
（３）ここから少し難しいですかね。原則の３つ目をフル活用して丁寧に解いていきます。

まずはHとJ、JとBは同じ面上にあるので、普通に線分で結べば大丈夫です。
結ぶと下の図のようになります。

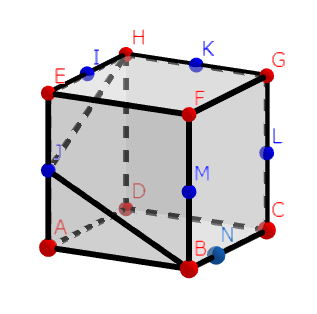
ここで、すこし工夫します。平面HDBFを取り出して書いてみます。HFとEGの交点をX、ACとBDの交点をYとします。すると、下の図のようになります。

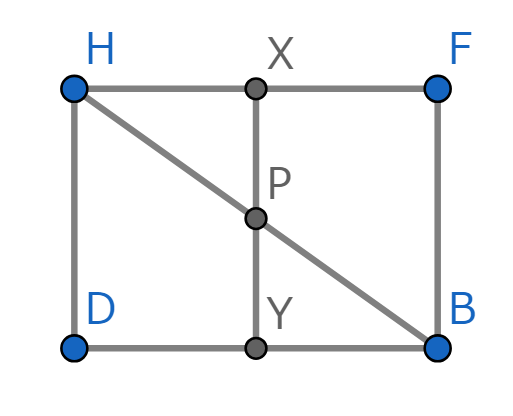
この平面上において、線分XYは、平面HDBFと平面EACGの交線となり、XYとHBの交点はXYの中点Pであるとわかります。ここで、平面EACGを取り出してみると、下の図のようになります。

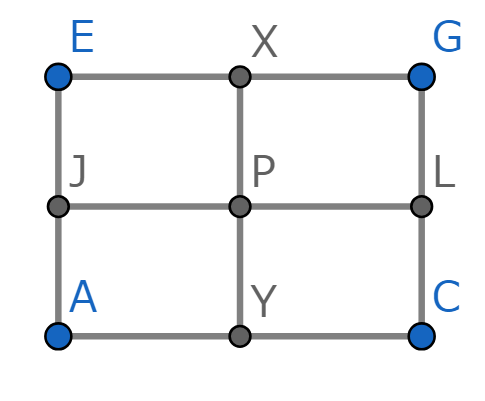
こうしてみると、JとPが切断面上にあるので、原則2から、反対側の点Lも切断面上にあるとわかりました。よって切断面は以下の図のようになります。

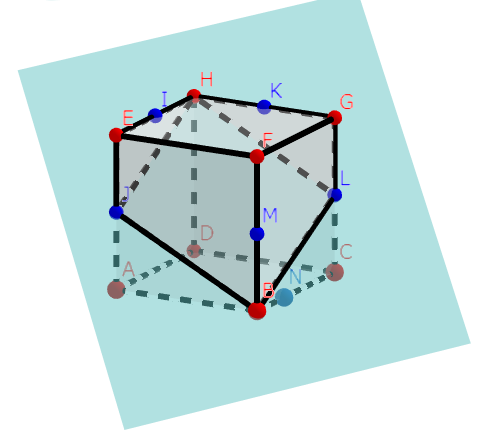
ここで、PはHとBの中点であるとともに、JとLの中点であるとわかります。よって、対角線が互いの中点で交わるので、切断面の四角形HJBLは平行四辺形だとわかります。これは、平面が、互いに平行な３辺それぞれの上にある３点を通るときに常に成り立ちます。証明は全く同じなので、自分で考えてみてください。これで原則３が示せましたね。

ところで、この四角形は４辺の長さが等しいです。一方で対角線の長さは異なるので、この四角形はひし形、が正解でした。平行四辺形と答えた方は残念。早とちりしないで、ゆっくり図を書いて考えてみるのが、上達への近道ですよ。

このように、立体の問題でも、立体内部のある平面を取り出して考えるとさらっと解けることは結構よくあります。立体図形の問題が難しいのは、立体把握が難しいからで、本質的には何も難しくないことが多いです。まずは難しい立体の問題は、立体に比べて簡単な平面の問題に落として考えるのが早いです。

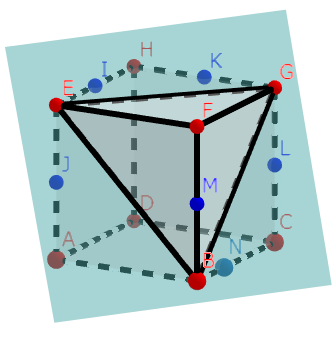
（４）原則３を使えるところで使うと、こんなめんどくさそうな問題でも、ちゃちゃっと解けちゃいますよ～

まずは与えられた点で同一な面上のものを結びます。この時、「面」は立方体の面のみを表すことに注意しましょう。「面」と「平面」をごっちゃにしないでくださいね。今回はIとJですね。すると下のような図が書けます。

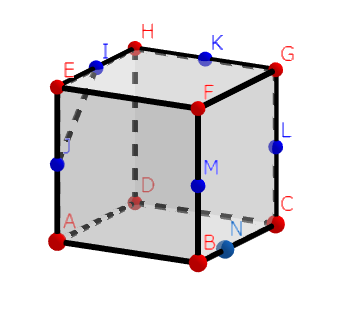
つぎに、LからIJと平行に線を引きます。

おっと、線を伸ばしすぎてしまいました。もう同一面上の点がないから困りましたね。しかし、よーく見ると、おや？

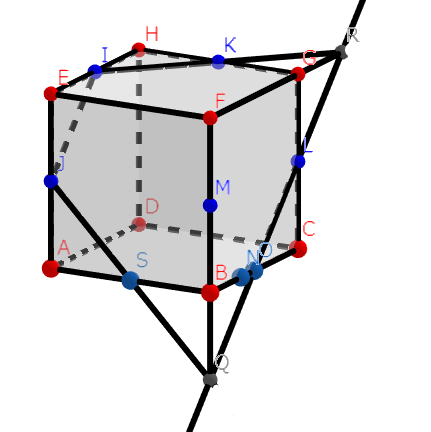
FBを延長した半直線と、直線LOは、点Qで交わります。すると、あら不思議、JとQは同一面上です！結んであげると、ABとの交点S（ABの中点：証明は簡単なのでご自分で）ができました。反対側も同じです。FGを延長した半直線と直線LOは点Rで交わり、RとIは同一平面上なので、IとRを結ぶと、HGと中点Kで交わりましたね。

あとは同一面上の点、SとO、KとLを結んでおしまいです。出来上がった切断面は下の図のようになります。

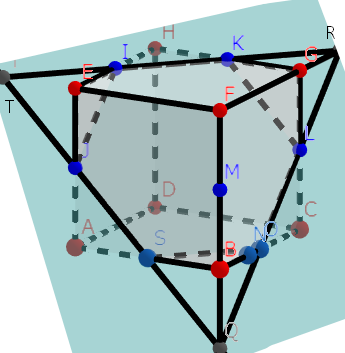
QSとRKの交点をTとすると、三角形TQRは正三角形で、青い点はその各辺を３等分しているので、この切断面は正六角形だとわかります。

このように辺を延長すると解決される問題は数多くあります。ぜひテクニックとして覚えておくといいでしょう。

（５）こちらは辺の延長で一発です。

まずは、「直線」IKを引きまして、同一面上の点を探します。

辺FE、FGを延長した点と上の直線との交点が、どちらもMと同じ面上にありますね。図は次の通り。

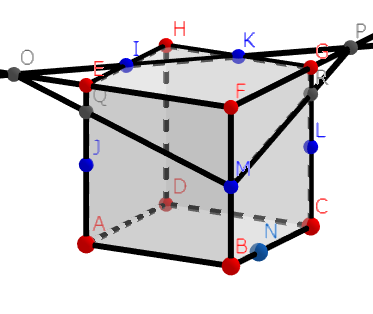
最後に、交点Q、RとI、Jを結べば完成です。図は以下。

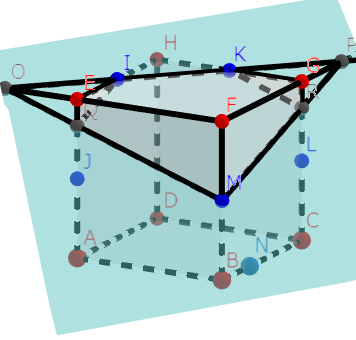
この五角形は辺の長さが違うので、答えは五角形、といったところですかね。

（６）これは難しいです。なぜ難しいかははじめにわかります。

まずは図を書いてみましょう。わかりやすくするために、関係ない点は消してあります。

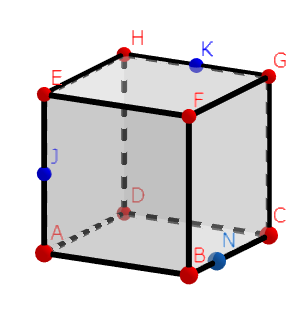
さあ見てください。まず最初にすることはなんでしたか？そう、切断面上かつ同一面上の２点を結ぶことでしたよね。

ところがこの図には切断面が通る同一面上の２点がありません。

どうしましょう。

こんな時は、とりあえず２点を結んでみるのがいい手です。例えばJとNを結んでみます。

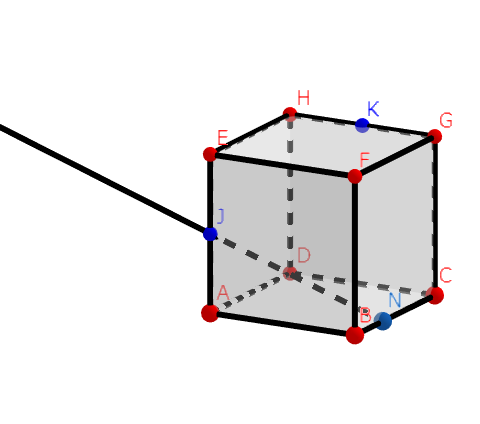
おっと、また伸ばしすぎてしまいました。目の錯覚のような図形が出来上がりました。さて、同一面上に２点ないかな、、、

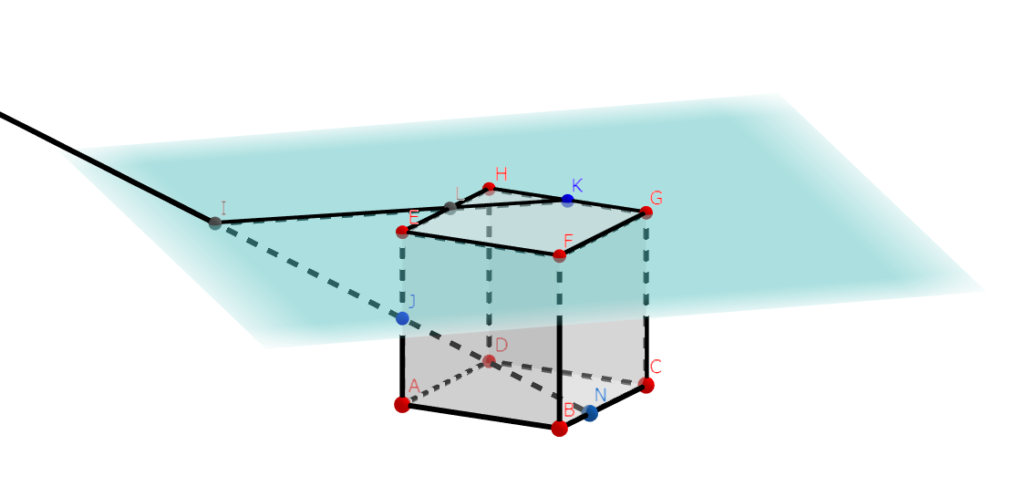
ありました。見えにくいですが、面EFGH上に点Iがあり、このIとKを結んだ線とEHとの交点がLです。

何が何だかわからない人は、下の真上から見た図を見るとわかると思いますよ。

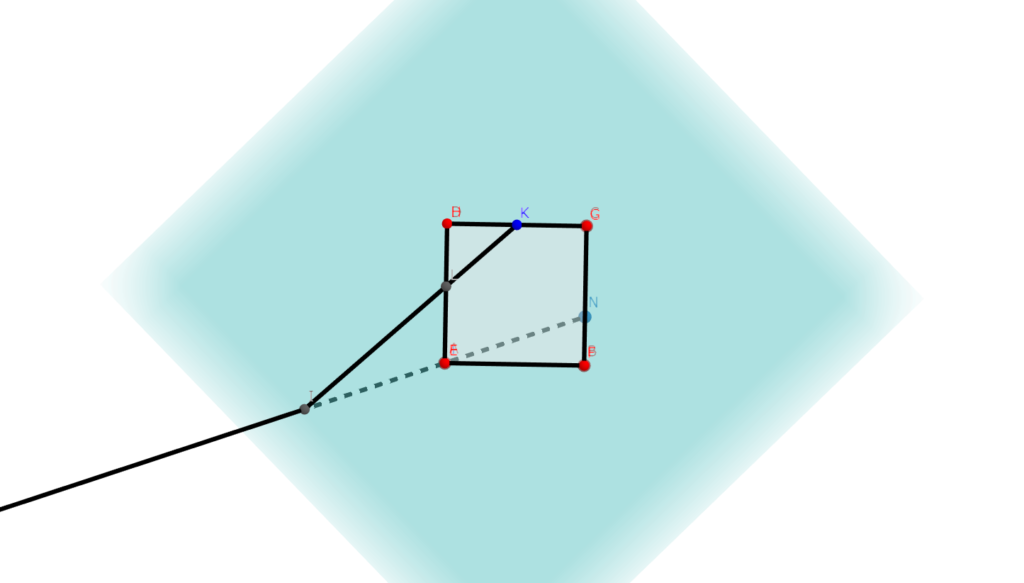
ここまで行ってしまえば、あとは辺の延長と原則3を使って終わりです。ここは省略するので、自分で頑張ってみてください。

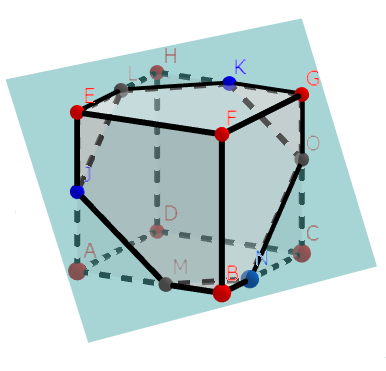
結果の図は下で、答えは(ただの)六角形になります。

さて、長かった例題も終わり、いよいよ本題に入りましょう。

今回の問題

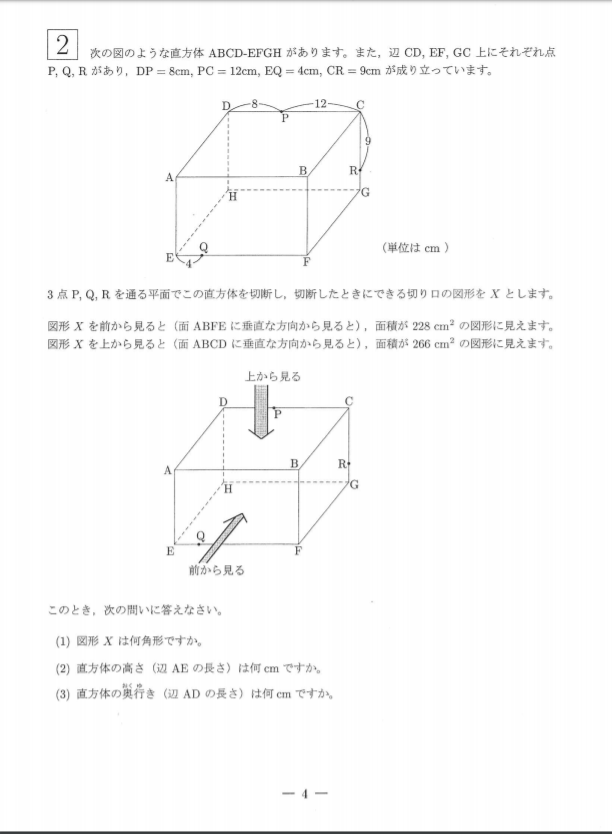
こちらの問題でしたね。ではまず、切断面Xから考察していきたいと思います。実はこの切断面Xは、本質的には例題の（４）と全く同じです。

（１）先ほどの例題（４）と同じように進めていきます。

まずは同一面上にある点、PとRを結びます。

その後、QからPRに平行な「直線」を引きます。

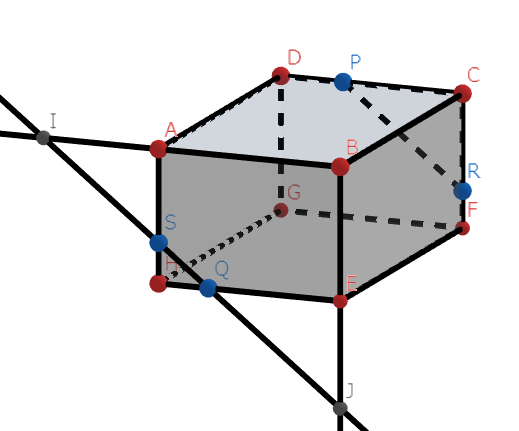
そして、同一面上のIとP、JとRを結びます。

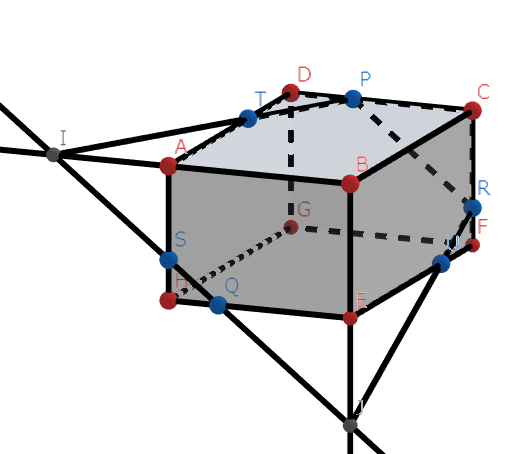
そして、残った2辺をつないで終わりです。

出来上がった図形は、青い多角形、そう、六角形でした。

（２）これは原則3で一発です。

原則3より、PRとSQは平行です。ここで、PCとHQも平行なので、
角CPR＝角HQSが成り立ちます。

また、角PCR＝角QHS＝90°なので、二角相等で、三角形PCRと三角形QHSは相似です。よって、対応する辺の比から、12:9=4:□で、HS＝３が成り立ちます。

ここで、六角形を前から見ると、下の図のようになります。

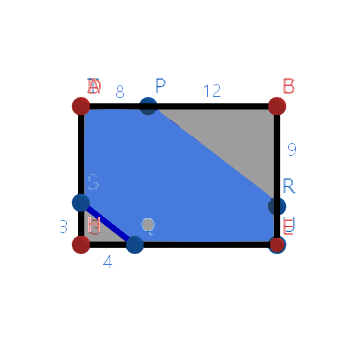
この図の書き方は、まず前から見た時の長方形を書いて、その後長方形の頂点や辺に重なる点を書き加えると書きやすいです。

この青い部分が228㎠ですから、長方形の面積は228+12*9/2+3*4/2=288㎠ですから、高さは288/(12+8)=14.4㎝ですね。

（３）これは（２）に比べてだいぶ面倒です。

まずは、下の図をよーく見てください。

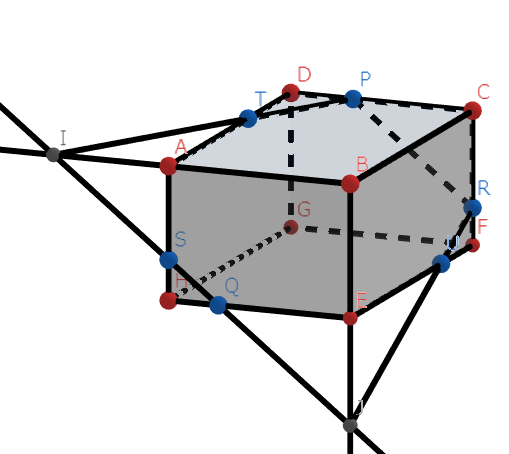
六角形を作図するときに使った図ですが、相似な三角形がたくさん隠れていますね。これを使って、AT：TDとEU：UFを求めます。

まず、三角形ASIと三角形HSQは相似なので、AI：AS＝HQ：HS。

AS＝AH－SH＝14.4ー3=11.4なので、AI＝11.4*4/3=15.2とわかります。

また、三角形TAIと三角形TDPも相似なので、AT：TD＝AI：PD＝19：10とわかります。

同様にして、三角形HQSと三角形EQJも相似なので、HS：HQ＝EJ：EQ。

EQ＝8＋12－4＝16なので、EJ＝16*3/4=12とわかります。

また、三角形UEJと三角形UFRも相似なので、
EU：UF＝EJ：FR＝12：(14.4ー9)=20：9とわかります。

そこで、上から見た図を書くと、下のようになります。

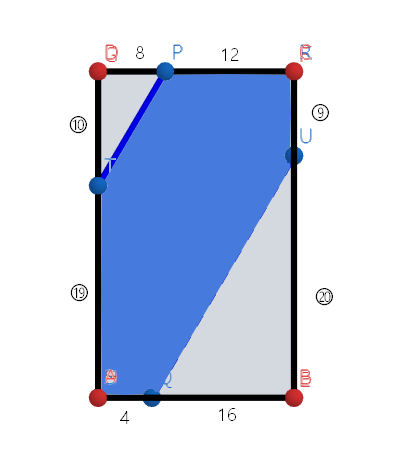
この図形の青い部分が266㎠なので、266＝㉙*20-⑳*16/2-⑩*8/2=①*380となり、①＝266/380=0.7とわかります。よって奥行きは㉙なので、0.7*29=20.3㎝とわかります。

今回のポイント

今回は立体の切断に関する問題でした。覚えておいてほしいことはたった３つ、立体切断の3つの原則、これにつきます。

再掲：立体切断問題　3つの原則

原則１：平面は通る３点を決めれば決まる

原則２：平面と平面の交線は直線

原則３：平行な２つの面に表れる切断面（直線）は互いに平行

この3つさえマスターできれば、立体切断は怖いものなしです。

最後まで読んでいただき、ありがとうございました。

この記事を書いたライター

東京受験

• インタビュー2021年11月20日【13の質問】あなたが医学部受験を決める理由＆受かる人の特徴とは？－医学部受験塾ACE Academy社長髙梨裕介さんインタビュー
• 受験対策・科目別勉強2021年9月18日「医学部予備校ACE Academy」体験記
• 勉強法&生活スタイル2021年7月29日【超必見】楽器練習ガチ勢へ。
• 豆知識・思うこと2021年7月1日【創立100周年！】中国共産党ってどんな党？

Tweet